3. CÁLCULOS; ESTADÍSTICA DESCRIPTIVA
La Estadística Descriptiva, describe, analiza y representa un grupo de datos utilizando métodos numéricos y gráficos que resumen y presentan la información contenida en ellos. En este caso, los resultados del análisis estadístico no pretenden ir más allá del conjunto de datos investigados, es decir, de la muestra o de la misma población de dónde hemos obtenido los datos.
Los cálculos dependen del modelo estadístico que se utilice. En general, y debido a su facilidad, se utilizarán modelos basados en la distribución normal.
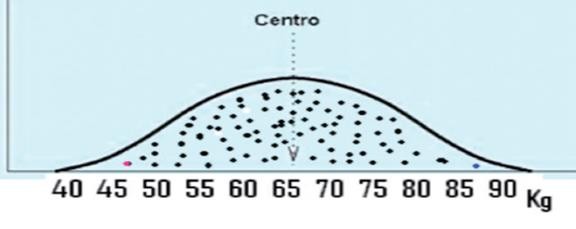
Una distribución no es más que una representación gráfica de los resultados obtenidos en una variable. Cuando la distribución de frecuencias es una curva de campana, se describe como distribución normal o de Gauss.
Por ejemplo, imaginemos que tenemos una muestra de 75 mujeres de 25 a 50 años de edad a las que hemos pesado. Cada punto que aparece en la gráfica es el peso de una mujer. Lo más habitual es que muchas pesen entre 55 y 75 Kg, por eso hay más puntos en esa zona. Cada vez que nos vamos hacia ambos lados de la gráfica, hay menos puntos, porque hay menos mujeres que pesen menos de 50 kg y también menos mujeres que pesen más de 80 kg. Cuando esto ocurre, es una indicación de que la distribución es simétrica o “normal”.
Los datos numéricos pueden resumirse por el cálculo de su tendencia central y de su variabilidad, mediante el cálculo de los porcentajes y las proporciones, y por medio del cálculo de razones y tasas. Los programas informáticos han facilitado estos cálculos.
3.1. Medidas de posición
3.1.1. Medidas de tendencia central
La medida de la tendencia central usada con mayor frecuencia es la media aritmética. Otras determinaciones de la tendencia central menos conocidas, pero también útiles, son la mediana y la moda.
La media, también llamada media aritmética, se obtiene mediante la suma de los valores individuales y su división entre el número total de mediciones. Se representa por µ (en poblaciones) o x (en muestras).
En su cálculo intervienen todos los valores de la distribución. Esto le hace muy sensible a la presentación de observaciones extremas o anómalas al hacer que la media se desplace hacia ellas.
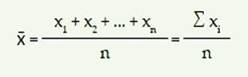
Por ejemplo, imaginemos en una muestra de 10 sujetos, la variable edad medida en años, nos ha dado los siguientes resultados: 25, 27, 31, 35, 38, 21, 40, 31, 33 y 36.
Media aritmética de los valores: Se suman los valores (25 + 27 + 31 + 35 + 38 + 21 + 40 + 31 + 33 + 36 = 317), dividiendola entre el número de valores (10). Por lo tanto: 317/10 = 31,7 años.
Si en la serie anterior, la última edad fuese 71 en lugar de 36, la media seria de 35,2 años.
La media aritmética tiene una serie de ventajas:
- Es fácil de calcular.
- Es única.
- •s el centro de gravedad de la distribución, por lo que es el índice de centralización más utilizado para realizar inferencias.
El principal inconveniente es la escasa representatividad que puede tener como valor central de la distribución, en el caso de que la variable tome valores anormalmente extremos, dando lugar a conclusiones no muy fiables. Sólo se puede determinar para variables cuantitativas.
La mediana de una distribución es un punto medio en el cual la mitad de las observaciones son inferiores a este valor y la otra mitad son superiores al mismo. Para su cálculo se ordenan los valores de la variable de menor a mayor, y se busca aquel valor que divide a la distribución de frecuencias de forma que el número de frecuencias que quedan a su izquierda es igual al número de frecuencias que quedan a su derecha. Coincide con el percentil 50 (véase más adelante).
Por ejemplo, la mediana de la serie: 1,2,4,5,5,6,6,8,9, es 5, ya que debajo de él quedan cuatro observaciones, y por encima otras cuatro.
Si la serie es par, la mediana es la media de los valores centrales. Por ejemplo, en la serie: 1,2,4,5,5,6,6,6,8,9; la mediana es la media de 5 y 6, es decir, 5,5.
Su cálculo resulta de gran utilidad en los siguientes casos:
- Cuando existan valores anormalmente bajos o elevados. Esta medida es menos sensible que la media aritmética cuando existen valores extremos, ya que en su determinación no intervienen todos los valores de la variable, sino los que ocupan las posiciones centrales.
- Cuando en las distribuciones agrupadas en intervalos el primero sea del tipo menor que, o el último sea del tipo mayor que, siempre y cuando ninguno de estos intervalos sea el intervalo mediano.
- Cuando se analizan variables cuantitativas medidas en escala ordinal, ya que en este caso no se podría determinar la media aritmética, siendo la mediana la medida de tendencia central más representativa. La mediana es de cálculo rápido y de interpretación sencilla. El principal inconveniente de la mediana es que tiene unas propiedades matemáticas complicadas, lo que hace que sea difícil de utilizar en inferencia estadística.
La moda es la determinación más frecuente en una distribución.
Por ejemplo, en la última serie del ejemplo: 1,2,4,5,5,6,6,6,8,9; la moda o el valor más frecuente es 6, que se da en tres ocasiones.
Tiene la ventaja de poder calcularse para todo tipo de variables, incluidas las cualitativas. La moda es la mejor medida de tendencia central en el análisis de los atributos medidos en escala nominal, ya que sus modalidades no son susceptibles de ser ordenadas, no admitiendo tampoco ningún tipo de operación algebraica, como por ejemplo; ¿Qué nombre es el que más se repite en una serie?, o ¿en qué ciudad han nacido más sujetos de la muestra?
Su inconveniente es que puede no ser única al existir varios valores que presenten la máxima frecuencia absoluta, teniéndose entonces una distribución bimodal (tiene dos modas), trimodal (tres modas), etc.
3.1.2. Medidas de tendencia no central
Los cuantiles, son aquellos valores de la variable que dividen a la distribución ordenada en partes, de tal manera que cada una de ellas contiene el mismo número de frecuencias. Así;
- Los cuartiles (i Q), dividen a la distribución en 4.
- Los deciles en 10.
- Los percentiles en 100.
Los más usados en Ciencias de la Salud son los cuartiles y los percentiles. Los cuartiles dividen a la muestra en 4 grupos con frecuencias similares.
- Primer cuartil = Percentil 25 = Cuantil 0,25
- Segundo cuartil = Percentil 50 = Cuantil 0,5 = Mediana
- Tercer cuartil = Percentil 75 = Cuantil 0,75
Los percentiles proporcionan otra manera de tener en cuenta las variaciones en las distribuciones. Igual que la mediana es el percentil 50 de una recopilación de datos, puede determinarse el percentil 75 o el 95, que indican que una medición determinada es superior a 75% o a 95% de todos los demás valores.
Una ventaja de los percentiles es que pueden aplicarse a los datos con una distribución asimétrica, no normal, en la que los datos no están distribuidos de manera uniforme alrededor de la media.
