5.3. Gráficos para variables cuantitativas continuas
- Histograma.
Se construye representado sobre cada intervalo un rectángulo que tiene este segmento como base. El criterio para calcular la altura de cada rectángulo es el de mantener la proporcionalidad entre las frecuencias absolutas (o relativas) de cada intervalo y el área de los mismos. Si los intervalos son de igual amplitud la altura puede coincidir con la frecuencia (absoluta o relativa). Si los intervalos son de distinta amplitud la altura se calcula dividiendo la frecuencia por la amplitud (frecuencia rectificada o densidad de frecuencias), que será la altura del rectángulo. - Polígono de frecuencias.
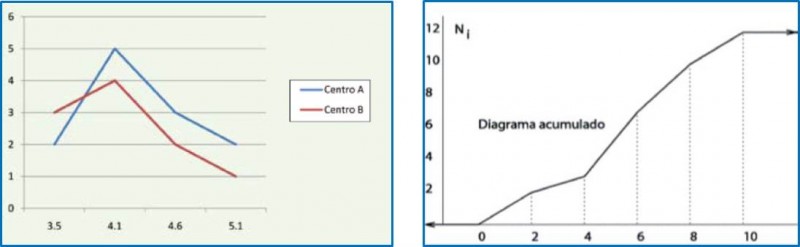
Se construye fácilmente si se representa previamente el histograma. Se unen mediante líneas rectas los puntos del histograma que corresponden a las marcas de clase. En el primer y último intervalo se considera que adyacentes a ellos existen otros intervalos de la misma longitud y frecuencia nula y se unen por una línea recta los puntos del histograma que corresponden a sus marcas de clase. Tiene en común con el histograma el que las áreas de las gráficas sobre un intervalo son idénticas. - Polígono de frecuencias acumulado u ojiva.
Se obtiene como la poligonal definida en abscisas a partir de los extremos de los intervalos y, en ordenadas, por alturas que son proporcionales a las frecuencias acumuladas. Deriva del histograma.
5.4. Diagramas Especiales
Son diagramas diferentes a los anteriores y suelen utilizarse con bastante frecuencia.
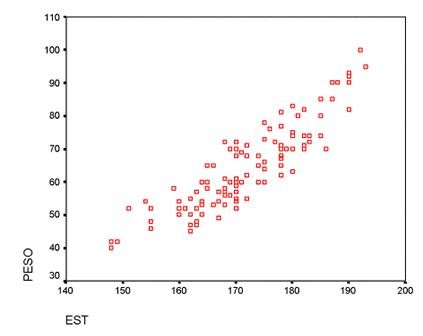
- Gráfica de dispersión.
Permite visualizar la distribución y la posible relación entre dos variables medidas en cada sujeto de la muestra.
- Gráficos Box plots (de caja “box” y bigotes “whisker plots”).
Permiten determinar fácilmente de forma visual la tendencia central, la variabilidad, la asimetría y la existencia de valores anómalos en una distribución de frecuencias.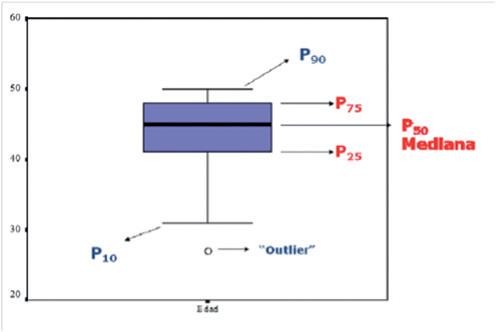
Incluye las siguientes características de la distribución:
o Caja (box): La línea interior representa la mediana, la de la izquierda el primer cuartil y la de la derecha el tercer cuartil. La caja recoge el 50% de las observaciones de la distribución y se determina uniendo los extremos de estas tres líneas por dos segmentos paralelos.
o Bigotes (whiskers): La observación más grande que no se aleja más de 1,5 mveces el recorrido intercuartílico (C3 – C1) desde el tercer cuartil se encuentra unida a la caja por el bigote derecho. La observación más pequeña que no se aleja más de 1,5 veces el recorrido intercuartílico desde el primer cuartil se encuentra unida a la caja por el bigote izquierdo.
o Valores sospechosos de ser anómalos (o): Los puntos que sobrepasan los extremos de los bigotes pero no están a más de 3 veces el recorrido intercuartílico desde el lado derecho e izquierdo de la caja. Estos valores deben ser considerados con prudencia.
o Valores anómalos: Puntos que se alejan del lado derecho e izquierdo de la caja más de 3 veces el recorrido intercuartílico. Estos valores pueden no considerarse como pertenecientes a la distribución estudiada. - Diagrama de barras de error. Representa intervalos de confianza.
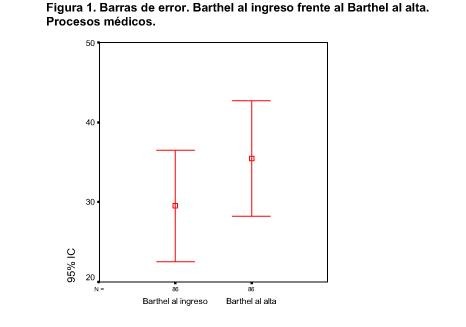
- Pirámide de población.
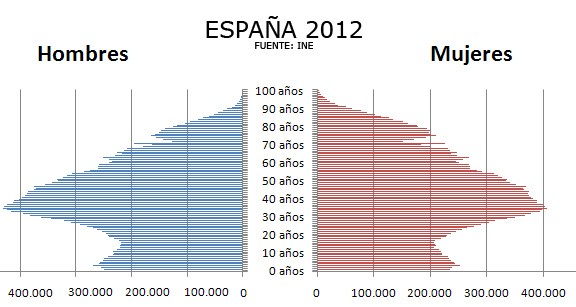
- Curvas ROC. Se usa para valorar la exactitud de una prueba diagnóstica. El área bajo la curva constituye el método más apropiado. Un parámetro para evaluar la bondad de la prueba es el área bajo la curva que tomará valores entre 1 (prueba perfecta) y 0,5 (prueba inútil). Puede demostrarse (Hanley y McNeil) que esta área se interpreta como la probabilidad de que ante un par de individuos, uno enfermo y el otro sano, la prueba los clasifique correctamente. En consecuencia, las curvas ROC son útiles para:
o Conocer el rendimiento global de una prueba. Área bajo la curva.
o Comparar dos pruebas o dos puntos de corte. Comparación de dos curvas o de dos puntos sobre una curva.
o Elegir el punto de corte apropiado para un determinado paciente.
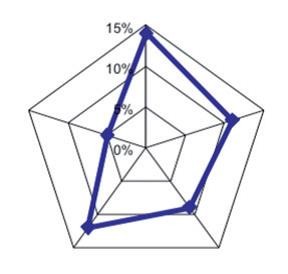
- Perfil radial. Representan frecuencias de una serie de casos. Cada “brazo” es una clase. En el ejemplo se representa el porcentaje de homosexuales en los cinco continentes (brazos).